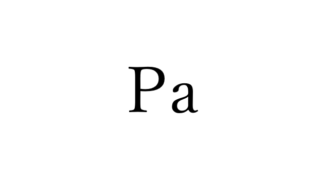平均自由行程

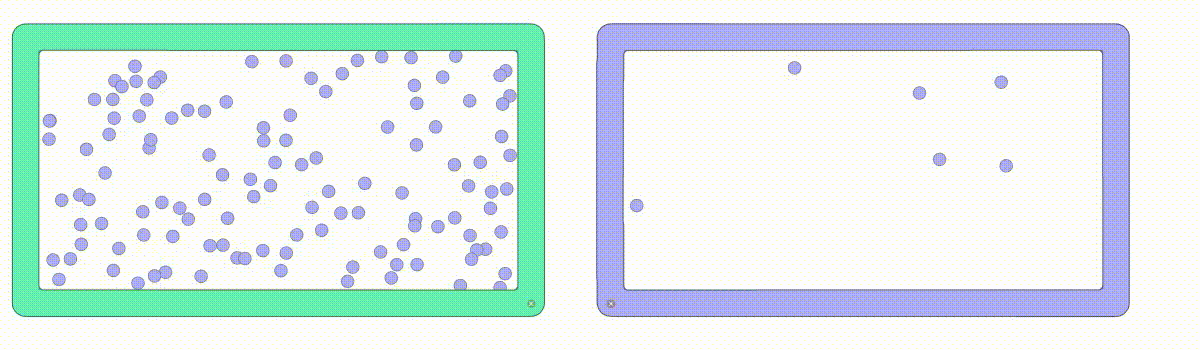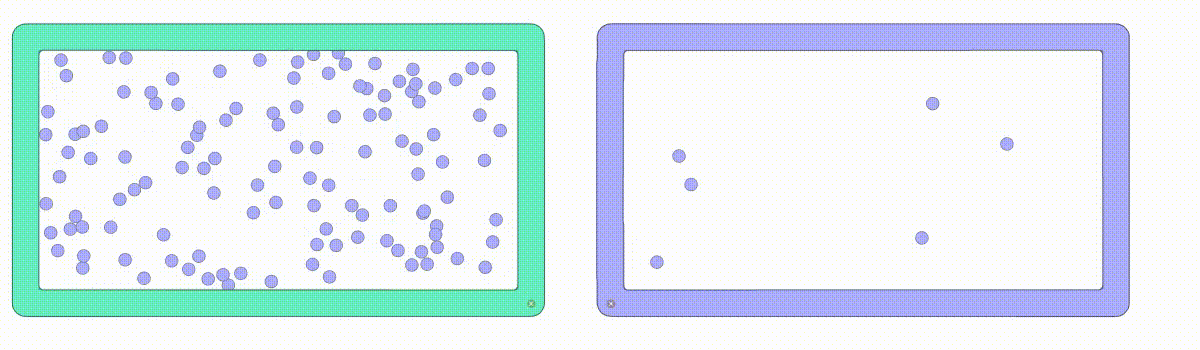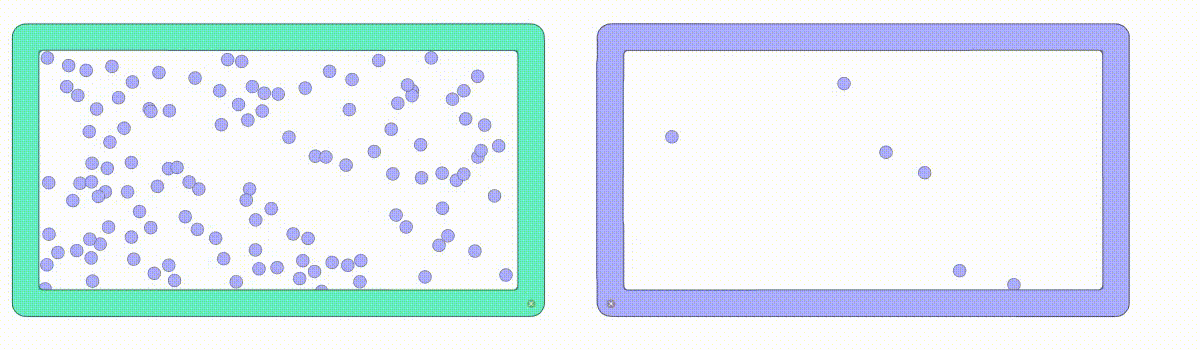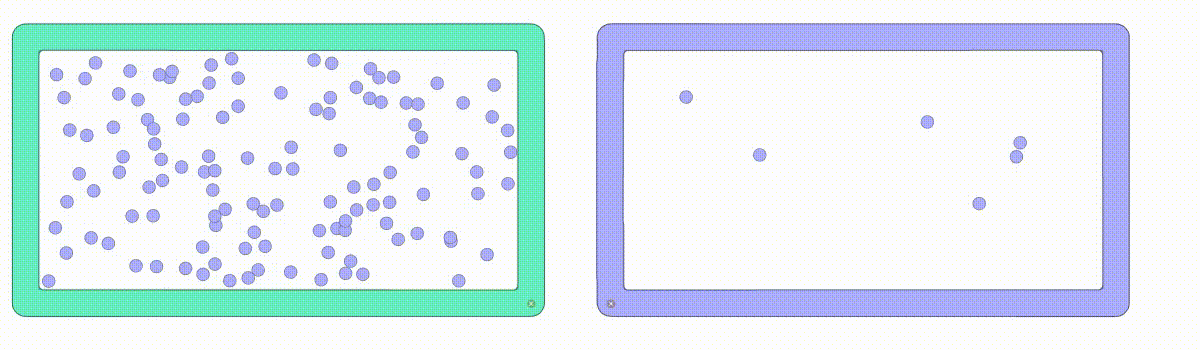
私たちの周りには空気があり、10cm×10cm×10cmの空間に2.6875×10²²個の気体分子があるということを真空の考え方で説明しました。この気体分子は自由に動き、気体分子同士で衝突しています。気体分子の数が多い場合と少ない場合では平均自由行程の距離が異なってきます。気体分子の数が1/10、1/100になると、平均自由行程は10倍、100倍になります。

平均自由行程の計算式

平均自由行程は下記の計算式で算出されます。

上記の数式を見ていただければわかる通り、平均自由行程は圧力が高くなると短くなり、圧力が低くなると長くなることがわかります。

Easy Copy Mathjax (nakaken88.com)

は、上記の式から1気圧の平均自由行程を求めてみましょう。
Tは温度ですが単位が[K]となっています。これはケルビンと言います。K[ケルビン]の詳しい説明は省きますが、これ以上冷えない温度が0Kと考えて頂ければ幸いです。真空も何もない空間を0Paとしたように、温度もこれ以上冷えない（物質の熱量がない）状態を0Kとしています。約-273℃が0Kです。ここではわかりやすいように300K（27℃）とします。

次はPです。Pは圧力になります。1気圧は約100,000Paです。

最後に分子直径になります。分子直径は3.74×10^-10mになります。

この様に計算式に値を代入する注意点として、使用する単位を合わせることが重要です。温度もセルシウス温度なのか、絶対温度なのか、圧力もPaなのか、Torrなのか、長さもmで良いのか…単位を合わせることが重要です。

\(　λ=3.11 \times 10 ^{-24} \frac{300}{100,000 \times （3.74 \times 10^{-10}）^2}　\)

となり、答えは6.67×10^-8mになります。66.7pm（ピコメートル）になります。1mmの百万分の一が1pmなので本当にわずかな距離という事になります。

真空中の平均自由行程

では、真空中の平均自由行程を考えてみましょう。100.000Paの時の平均自由行程が6.67×10^-8mなので、1Paの時の平均自由行程は6.67×10^-3m…つまり、6.67mmになります。